Mathics and Nebo

Symbolic Mathematics and AI Handwriting Recognition

June 13, 2022 · John Peach

Louis, I think this is the beginning of a beautiful friendship. - Rick Blaine, Casablanca

I’ve been playing around with a couple of fun math toys recently, Mathics and Nebo. Mathics is a free, open-source symbolic calculator. Nebo is a note-taking app for laptops, tablets, and smartphones with stylus inputs, and it can accept and understand mathematics. Nebo is free for the iPad, ($10 on Windows), and you can try Nebo here.

Sometimes you need to solve complex equations or plot functions. Other times you’re scribbling notes and derivations, because handwriting is just easier than typing out the LaTeX notation. Traditional digital tools often force us to choose between handwriting and computation, or require us to learn specialized syntax just to write basic equations.

This article introduces two complementary tools that bridge this gap, Mathics and Nebo. Mathics handles symbolic mathematics system doing everything from basic arithmetic to complex algebraic manipulations. If you’ve used Mathematica you’ll find that Mathics offers many similar capabilities at no cost.

Nebo, on the other hand, is a note-taking app that excels at recognizing handwritten mathematics. For those of us who prefer to work out problems by hand, Nebo can convert our natural mathematical handwriting into cleanly formatted equations. Whether you’re deriving equations, solving problems, or taking notes in a mathematics class, Nebo lets you write naturally while maintaining the benefits of digital organization and searchability. It can even solve basic equations directly from your handwriting. Nebo is free for the iPad, ($10 on Windows), and you can try Nebo here.

Together, these tools provide a flexible way to do mathematics. Use Nebo for initial note-taking and problem-solving, then switch to Mathics when you need more computational power or want to explore solutions symbolically. I’ll also describe the note-taking app Obsidian and a tool called SyncThing that keeps folders synchronized between devices so you can switch between your desktop computer and your laptop without losing any of your work. Let’s look at how each tool works and how they might help with your STEM problems.

Mathics

The description of Mathics says,

Mathics is a free, open-source general-purpose computer algebra system featuring Mathematica®-compatible syntax and functions.

It relies on Python libraries, in particular, Sympy for symbolics, mpmath for arbitrary precision floating-point arithmetic, MathJax to render equations, and three.js and Asymptote to create graphics. Mathics isn’t as powerful as Mathematica, but the price is much better. Here’s a problem we can try in Mathics,

x=i+1i+1i+1i+…x = i + \frac{1}{i + \frac{1}{i + \frac{1}{i + \ldots}}} \\

Find xx.

Notice that everything in the denominator of the first fraction is identical to xx, so the equation can be rewritten as

x=i+1xx2=ix+1x2−ix−1=0\begin{aligned} x &= i + \frac{1}{x} \\ x^2 & = ix + 1 \\ x^2 &- ix - 1 = 0 \end{aligned}

Using the quadratic formula,

x=i±i2−4(−1)2=i±−1+42=i±32.x = \frac{i \pm \sqrt{i^2 - 4(-1)}}{2} = \frac{i \pm \sqrt{-1+4}}{2} = \frac{i \pm \sqrt{3}}{2}.

In Mathics, the symbol for the imaginary unit i=−1i = \sqrt{-1} is II, so to solve for xx type

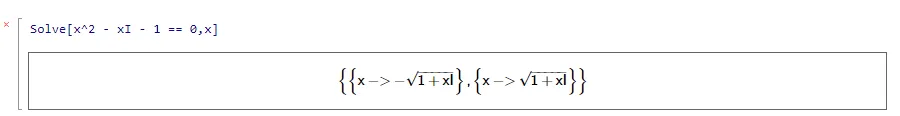
x2-Ix-1
Figure 1.

Mathics solution to the quadratic problem.

followed by Ctrl-Enter to get the solution. Hmmm. These solutions are correct, but not informative. The solution for xx has an xx in it.

The roots of a polynomial are the values of xx that make the polynomial zero, in this case, x2−ix−1=0x^2 - ix -1 = 0. An nth−n^{th}-degree polynomial will always have nn roots, even if some are complex (real + imaginary parts). Suppose the two roots to this polynomial are rr and ss, which means that

x2−ix−1=(x−r)(x−s).x^2-ix-1 = (x-r)(x-s).

Putting this into Mathics and collecting terms,

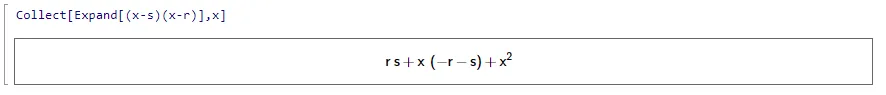
expand-rs
Figure 2.

Polynomial expansion in Mathics.

Then rs=−1rs = -1 and −r−s=−i⇒r+s=i-r-s = -i \Rightarrow r + s = i. Solving these two equations simultaneously in Mathics,

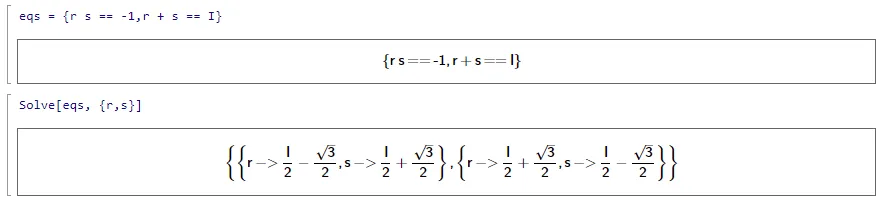
rs-simul
Figure 3.

Mathics solution to the polynomial problem.

which is correct.

To open a help window in Mathics, click on the ? in the upper right corner. Complete documentation is available online here.

Mathics-help
Figure 4.

The Mathics workspace and access to the help window.

Nebo

MyScript Nebo uses AI to interpret handwriting. If you have a tablet or laptop that accepts input from a stylus, Nebo will convert your handwritten notes to text. With Nebo, you can draw diagrams, and it will clean them up:

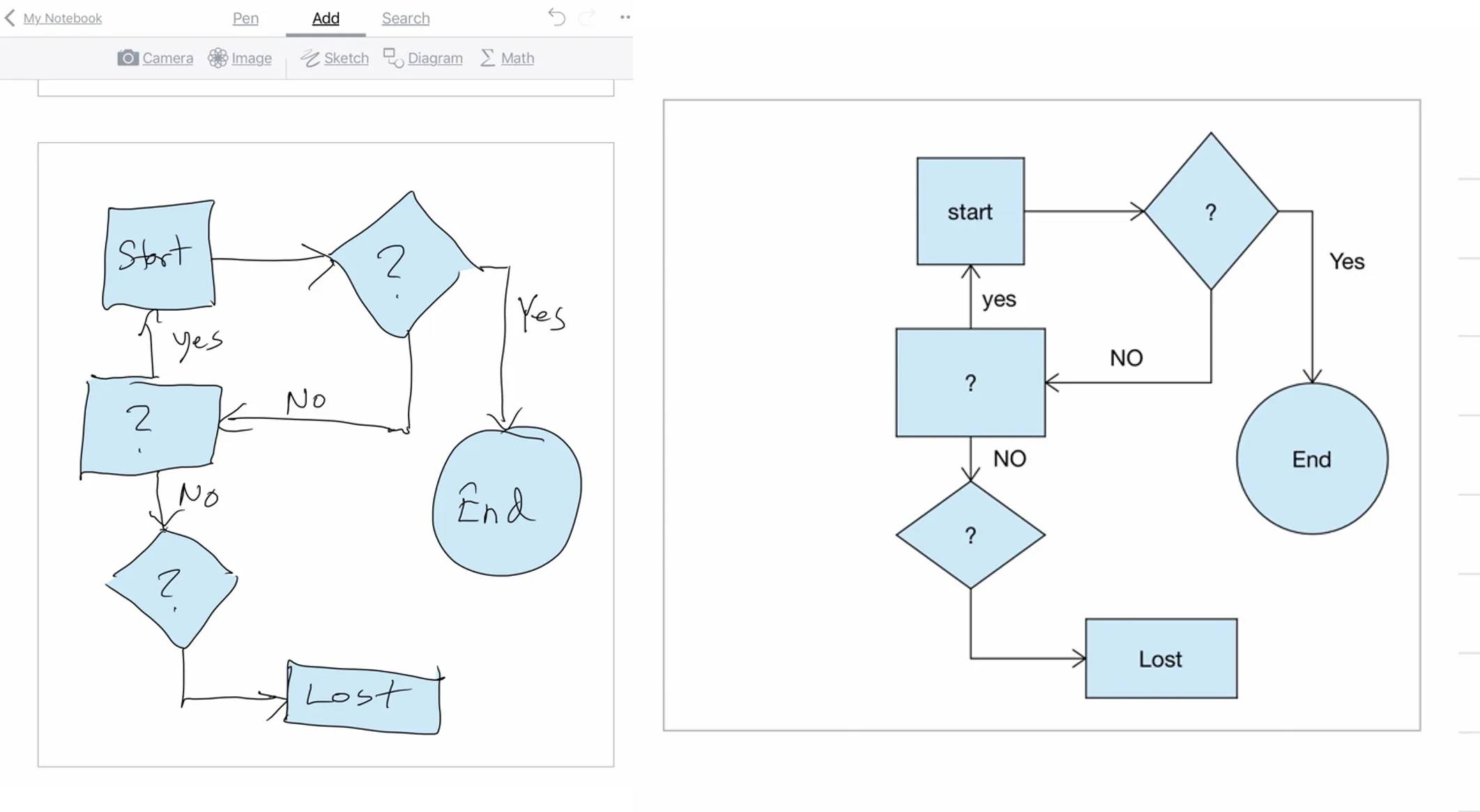
nebo-diagram
Figure 5.

Nebo converts hand-drawn sketch into a diagram.

You can insert images into a document, and draw freehand sketches. I tend to write ideas down on a pad of paper, and the next great idea goes on the next empty page in the pad. My house is cluttered with pads. What was this one all about?

notes
Figure 6.

My cluttered handwritten notes.

So I thought Nebo might be useful in organizing and cleaning up all my scribblings. Here’s an example:

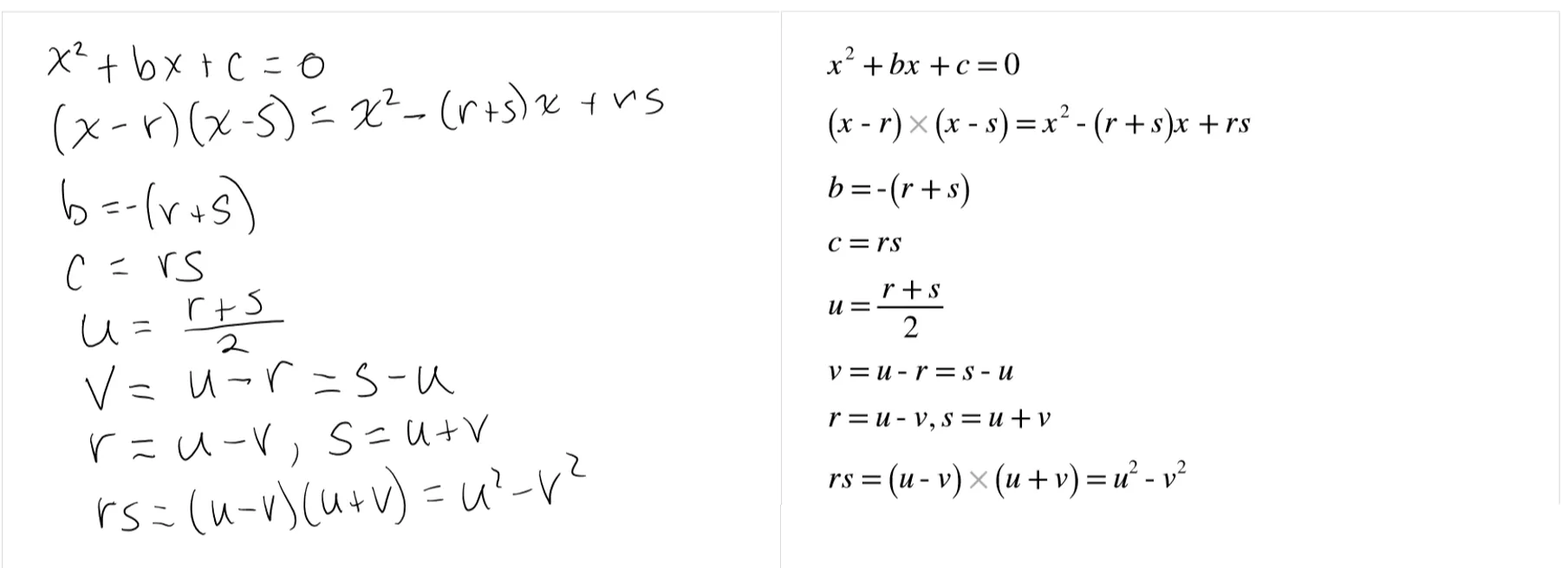
nebo-script-to-tex
Figure 7.

Handwritten version of the Mathics problem converted by Nebo.

On the left are the original hand-written equations. After tapping twice on the screen, Nebo converted everything to MathJax format. I had to fix three errors - two of the lower case vv‘s had been changed to upper case, and one of the rr‘s was interpreted as an nn. Other than that, Nebo got it exactly right on the first try.

If you copy a section of math in Nebo, you can paste it into a markdown editor like this.

x2+bx+c=0(x−r)×(x−s)=x2−(r+s)x+rsb=−(r+s)c=rsu=r+s2v=u−r=s−ur=u−v,s=u+vrs=(u−v)×(u+v)=u2−v2\begin{aligned} x^{2}+bx+c&=0\\ \left( x-r\right) \times \left( x-s\right) &=x^{2}-\left( r+s\right) x+rs\\ b&=-\left( r+s\right) \\ c&=rs\\ u&=\dfrac{r+s}{2}\\ v&=u-r=s-u\\ r&=u-v,s=u+v\\ rs&=\left( u-v\right) \times \left( u+v\right) =u^{2}-v^{2} \end{aligned}

Nebo includes the formatting characters

\begin{aligned}
x^{2}+bx+c&=0\\
\left( x-r\right) \times \left( x-s\right) &=x^{2}-\left( r+s\right) x+rs\\
b&=-\left( r+s\right) \\
c&=rs\\
u&=\dfrac{r+s}{2}\\
v&=u-r=s-u\\
r&=u-v,s=u+v\\
rs&=\left( u-v\right) \times \left( u+v\right) =u^{2}-v^{2}
\end{aligned}

I added ampersands before the equal signs to align each equation with the one above it. Nebo did all of the rest, including the \begin{aligned} and \end{aligned}.

Getting back to the math, to find the roots of the quadratic polynomial f(x)=x2+bx+cf(x) = x^2 + bx + c, you might remember the quadratic formula,

x=−b±b2−4c2.x = \frac{-b \pm \sqrt{b^2 - 4c}}{2}.

If you have the form f(x)=ax2+bx+cf(x) = ax^2 + bx + c, divide by aa and calling ba\frac{b}{a} the new bb, and ca\frac{c}{a} the new cc, which has the same roots.

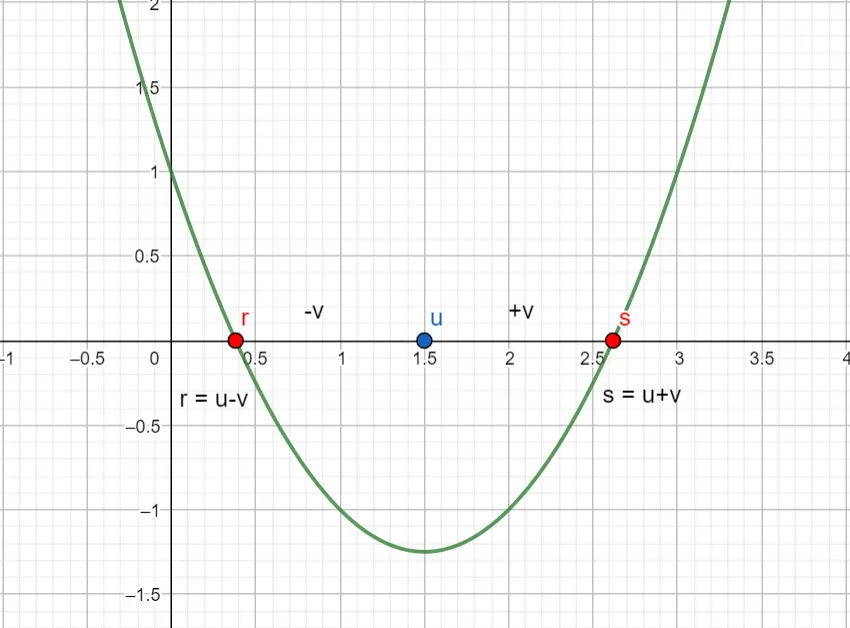
fx-GeoGebra
Figure 8.

Graphical solution to the quadratic problem.

If we call the roots rr and ss, then the plot of f(x)f(x) will cross the x−x-axis at rr and ss, and ff can be written as

f(x)=x2+bx+c=(x−r)(x−s).f(x) = x^2 + bx + c = (x-r)(x-s).

Expanding the terms on the right,

f(x)=(x−r)(x−s)=x2−(r+s)x+rsf(x) = (x-r)(x-s) = x^2 - (r+s)x + rs

which means that b=−(r+s)b = -(r+s) and c=rsc = rs.

Let’s call the midpoint between rr and ss the point uu. Then

u=r+s2u = \frac{r+s}{2}

or

u=−b2.u = -\frac{b}{2}.

Since uu is the midpoint, the distance from uu to ss is the same as the distance from rr to u,u, so let’s call that distance vv. Another way to express this is u=r+vu = r + v and s=v+us = v + u. Solving for rr in the first equation, r=u−v.r = u-v. Since c=rsc = rs then

c=rs=(u−v)(u+v)=u2−v2.c = rs = (u-v)(u+v) = u^2 - v^2.

After calculating uu in terms of bb, we can get vv from cc and uu,

v=u2−c.v = \sqrt{u^2 - c}.

To recap, first find the midpoint of the unknown roots which will be at −b2-\frac{b}{2}, and then get the distance to the roots which is u2−c\sqrt{u^2-c}. The roots will be v±uv \pm u. So, now you can follow all of my chicken-scratching in Nebo.

For example, suppose f(x)=x2−3x+1f(x) = x^2 - 3x + 1, the plot in the figure above drawn in GeoGebra. Then u=−32u = -\frac{3}{2} and

v=(−32)2−1=94−1=94−44=52.v = \sqrt{\left( -\frac{3}{2} \right)^2 - 1} = \sqrt{\frac{9}{4} - 1} = \sqrt{\frac{9}{4}-\frac{4}{4}} = \frac{\sqrt{5}}{2}.

So, the roots are

x=32±52=3±52.x = \frac{3}{2} \pm \frac{\sqrt{5}}{2} = \frac{3 \pm \sqrt{5}}{2}.

One more Nebo trick - write the equation with an equal sign at the end like this:

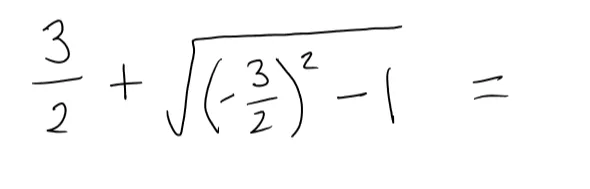
root-handwritten-Nebo
Figure 9.

Nebo solves equations with equals signs.

Double-tap, and you’ll get a neatly written equation with the solution!

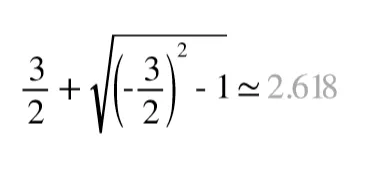
root-solution-Nebo
Figure 10.

Numerical solution.

Erase the ++, replace it with a minus sign, and double-tap to get the other root r≈0.382r \approx 0.382. Nebo doesn’t do complex math, so we wouldn’t be able to solve the problem done earlier in Mathics, but for quick calculations, it’s pretty neat!

A nice introduction to Nebo is available from Paperless and Vojislav Dimitrijevic of My Deep Guide reviews the mathematical capabilities here.

Obsessed with Obsidian

Obsidian is the electronic version of my pads of paper. Obsidian is a markdown editor and a knowledge database of your ideas linked together. Upmath shows how to get started using LaTeX in Markdown files to write equations. Help is available by clicking on the ? in the lower left-corner, which opens a new pop-up window. An outline appears in the left panel, and document links are shown in the right panel.

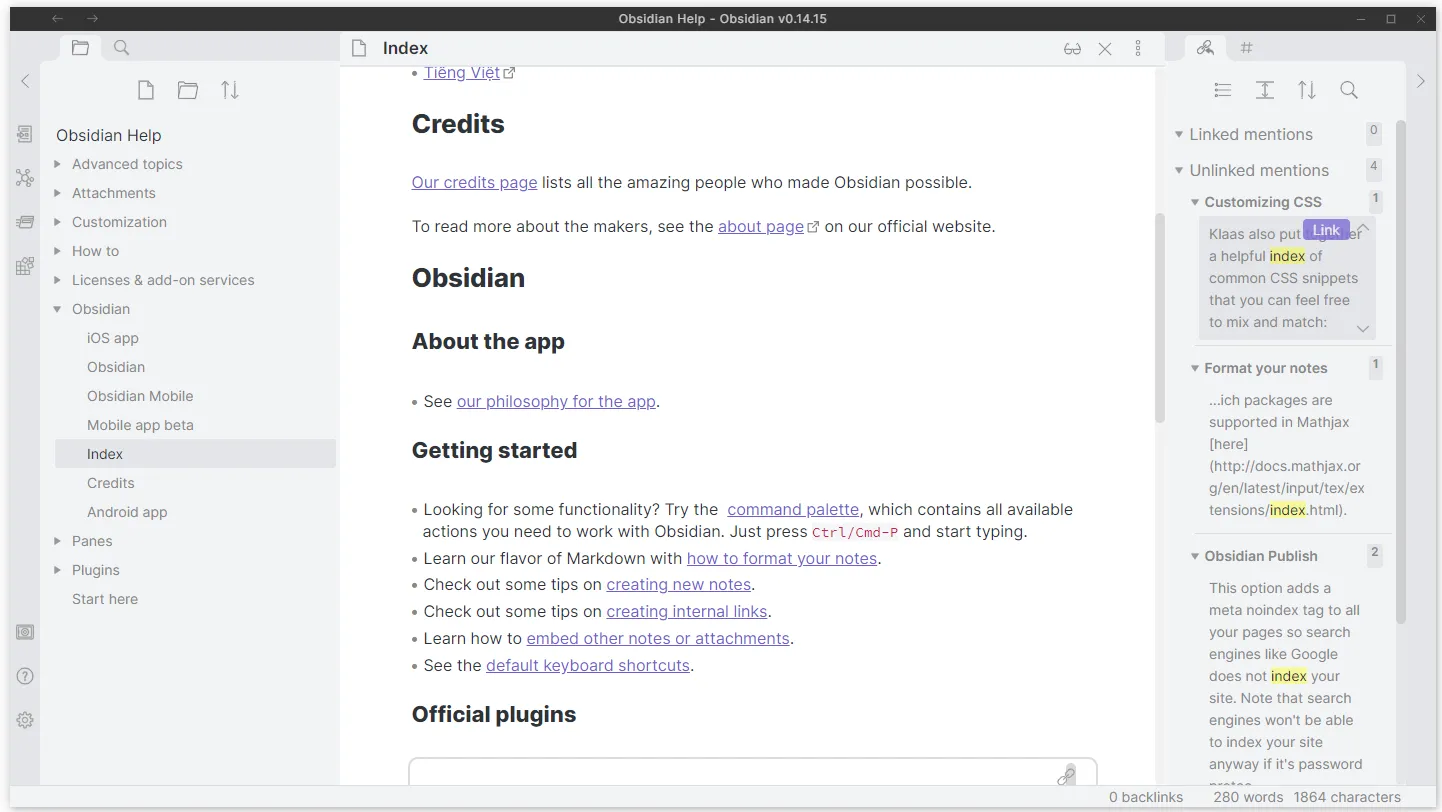
obsidian-help
Figure 11.

Obsidian note taking app.

The graphical view of help looks like this:

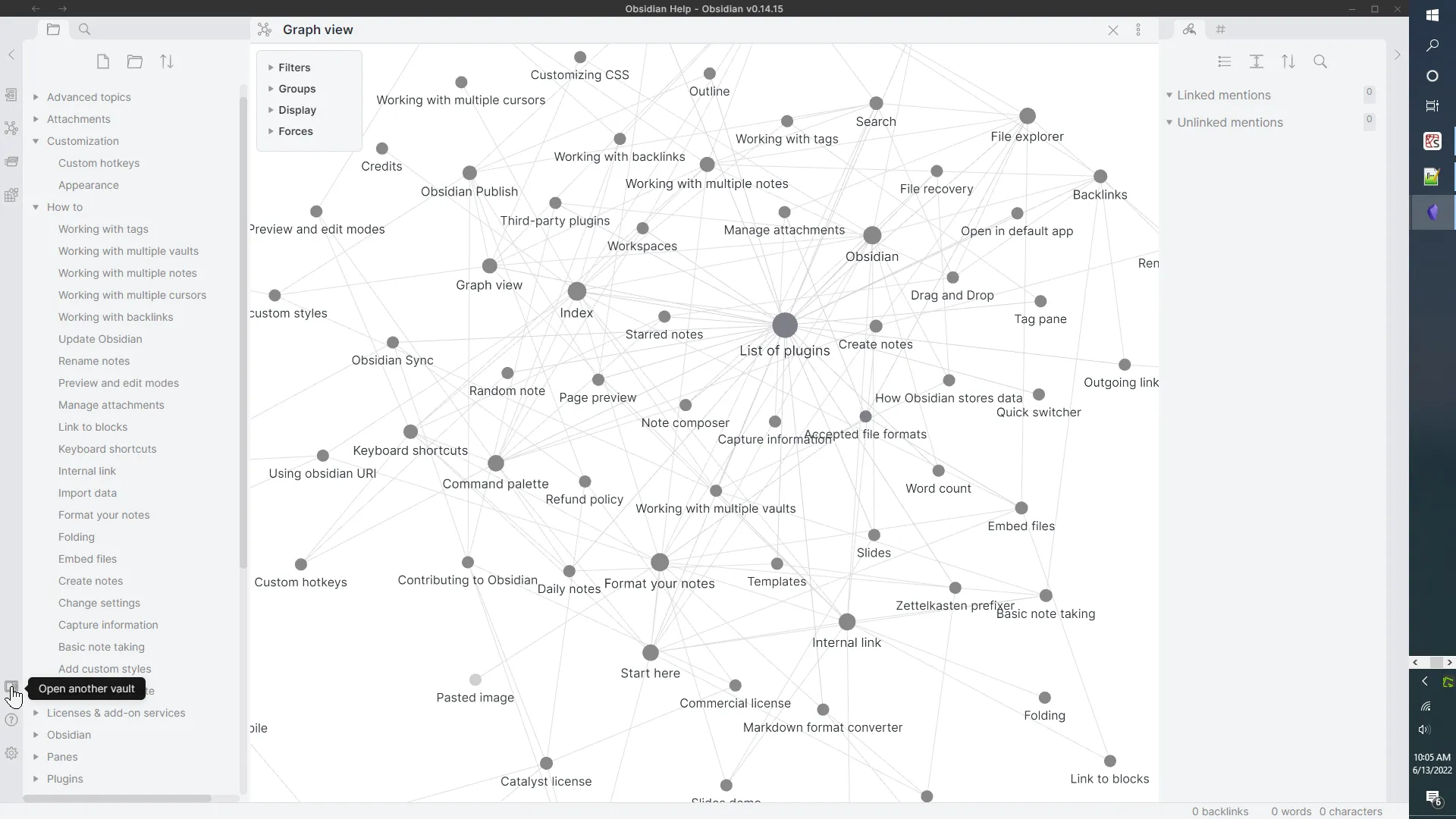
obsidian-help-graph-view
Figure 12.

Graphical view of your notes in Obsidian.

Click on Open another vault to switch to your files. To extend the capabilities of Obsidian there are both core plugins and community plugins. The Sweet Setup blog lists some of their favorite plugins, and LibHunt lists the top community projects.

SyncThing

I switch between the desktop computer and laptop frequently, depending on whichever is the most convenient at the moment. But, how should I keep files synchronized between the two? Copying back and forth whenever I modify a file on one seemed tedious.

floppy
Figure 13.

A floppy disk. How data used to be stored on computers after we evolved from cassette tapes.

This is where SyncThing comes to the rescue. It continuously synchronizes files between any number of your computers, all in the background, using your home network. Take a look at the “Getting Started” page, and online documentation. After installation, all you need to do is identify your computers and the folders you’d like to synchronize. After that, the software keeps everything up-to-date.

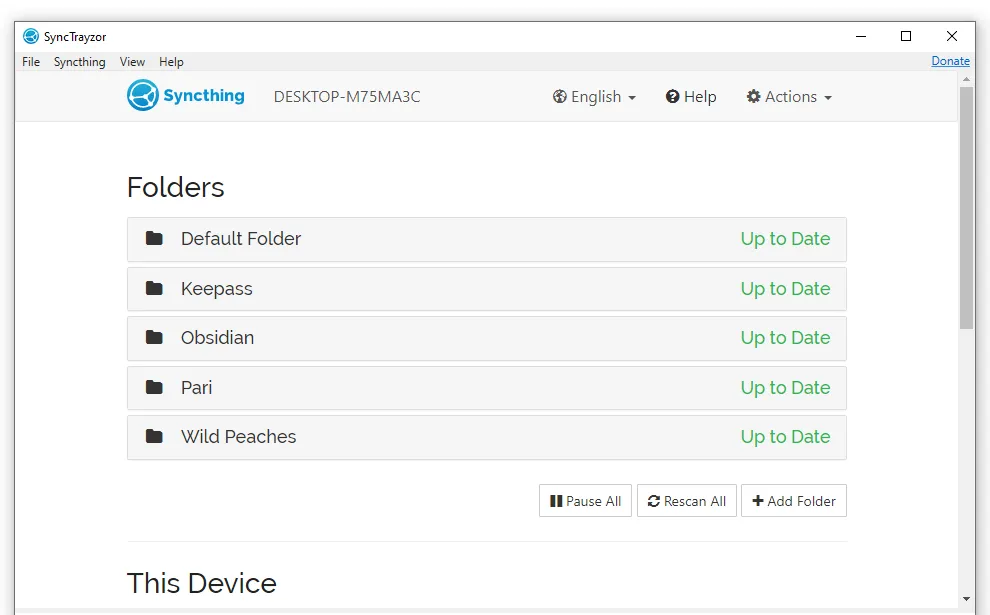
SyncThing
Figure 14.

SyncTrayzor synchronizes data between devices.

For Windows users, SyncTrayzor is a tray utility for SyncThing.

After installing SyncThing on both computers, I realized I needed to have both running simultaneously to be able to sync, but I almost always shut down one when working on the other. The solution is that SyncThing is available for both Android and iOS phones, using the same convenient GUI.

Since my phone is almost always on, it keeps the latest version of all the files from whichever computer I’m currently using. I’ve even found that Python code is automatically reloaded in the Spyder editor, so long as I’ve remembered to save my work.

Now, with the phone acting as an intermediary, SyncThing makes switching between computers indistinguishable from magic.

The Beginning of a Beautiful Mathematical Friendship

The tools we’ve explored form a handy system for mathematical work and note-taking. Each addresses a specific need while complementing the others:

Mathics provides the computational engine, letting you solve complex mathematical problems and explore solutions symbolically without the cost of commercial alternatives. When you need to verify a calculation, plot a function, or manipulate equations, Mathics offers a capable open-source solution.

Nebo bridges the gap between handwritten mathematics and digital notation. For those of us who think best with pen in hand, Nebo’s AI-powered handwriting recognition transforms our natural mathematical notation into cleanly formatted digital equations. Whether you’re working through derivations, taking notes in class, or sketching out ideas, Nebo preserves the fluidity of handwriting while adding the benefits of digital organization.

Obsidian serves as the knowledge hub, connecting all your mathematical notes, derivations, and insights. Its markdown support means you can seamlessly incorporate both Nebo’s exported equations and Mathics’ calculations into your notes, while its linking capabilities help you build connections between related concepts. Think of it as your digital mathematical notebook, but one where every page can be instantly found and every concept is connected.

SyncThing ties everything together by keeping your work synchronized across all your devices. No more emailing files to yourself or wondering which device has the latest version of your notes. Whether you’re working at your desk, on your laptop, or reviewing notes on your phone, SyncThing ensures you always have access to your complete mathematical workspace.

Together, these tools create a workflow that combines the best of both worlds: the natural feel of handwritten mathematics with the power of digital computation and organization. While each tool is valuable on its own, their combination provides a comprehensive environment for mathematical thinking, computation, and note-taking that adapts to your preferred way of working.

The best part? This entire ecosystem is built on free, open-source software (except for Nebo’s modest one-time fee on some platforms), making it accessible to students, educators, and mathematics enthusiasts alike. Whether you’re studying advanced mathematics, teaching others, or simply exploring mathematical ideas for fun, these tools provide a flexible and powerful platform for your mathematical journey.

Mathics Installation

Installing Nebo, Obsidian, and SyncThing is just a matter of following their instructions. Mathics is slightly more complicated but still easy. Here are the steps I used:

  1. Start Anaconda Powershell as administrator. I use Anaconda Python.
  2. Check python version: python —version
  3. Check pip version: pip —version
  4. Install Mathics: pip install Mathics-omnibus[full]
  5. Type: mathicsserver —help to check the installation
  6. Start mathics: mathicsserver
  7. In your browser (Chrome or Firefox) go to localhost:8000
  8. Save the mathics.png image from https://github.com/Mathics3
  9. Convert the image to mathics.ico using https://www.icoconverter.com/
  10. Make a batch file called mathics.bat containing the single command mathicsserver
  11. Create a desktop icon linked to mathics.bat, and change the icon to mathics.ico
  12. Click on the desktop icon to start Mathics, and type localhost:8000 in the address bar. Drag to the bookmarks bar.

Running Mathics from now on requires two steps - clicking on the icon to start the server followed by clicking the link to localhost:8000.

Software

References

Image credits