CAS with Geogebra

or, What's my radius?

April 02, 2024 · John Peach

Geogebra is a great tool for working with geometric objects, but it also has a computer algebra system (CAS) built in. There are other more capable computer algebra systems such as wxMaxima and Wolfram Language, but this might work for solving a simple algebraic-geometry problem.

Here’s the problem to solve: A circle touches the function $f(x) = x - x^3$ in two places, the origin and one other point. What’s the radius of the circle?

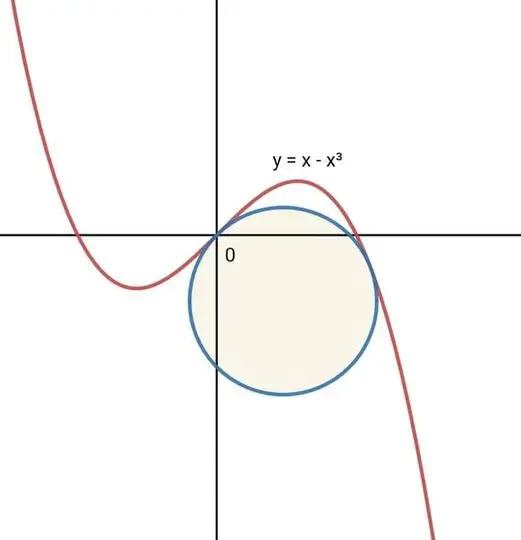
circle-problem — Figure 1.
Circle radius problem.

At the two points where the circle touches the function, lines perpendicular to the tangents and drawn from those two points will intersect at the center of the circle. What’s a tangent? Imagine a straight line that just touches the function at one point, and has the same slope that the function has at that point. To calculate the slope we need to find the derivative of the function.

The derivative

The derivative of a function is defined as $f'(x)$ where

f'(x) = \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}.

What this means is that you should choose some small number $\Delta x$ and calculate the value of the function at the point $x$ but shifted by $\Delta x$ , and then subtract the value of $f(x)$ , or the change in $y$ values. Divide by the difference in the $x$ values, which is $\Delta x$ to give the rise over the run, or the slope of the function at the point $x$ .

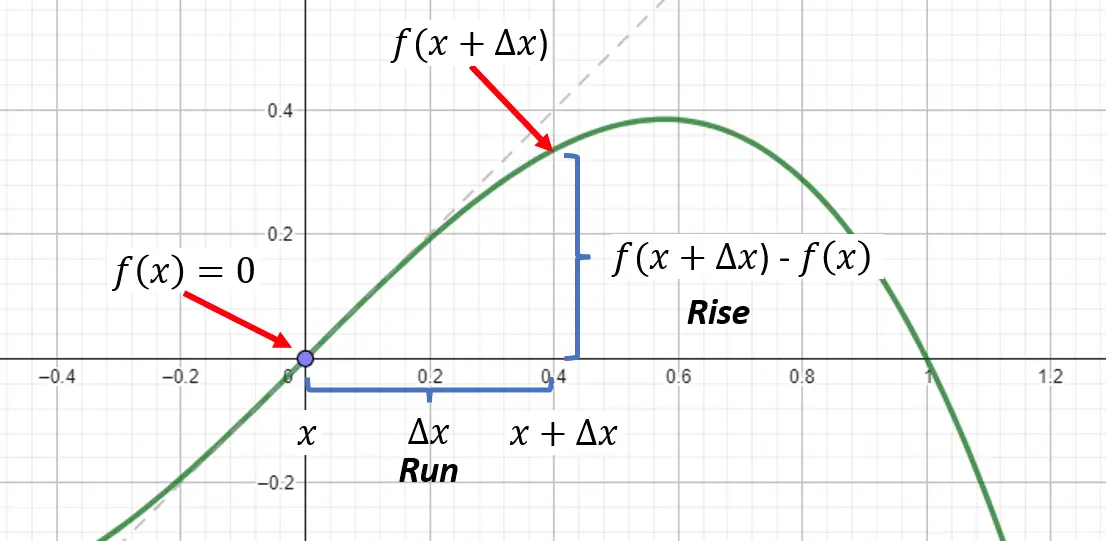
derivative-calculation — Figure 2.
Calcluating the derivative.

Now, let the step $\Delta x$ shrink down to practically nothing and see what the rise over the run is for $\Delta x \approx 0$ to get the slope of the function at a point, which is also the derivative of the function. Let’s see how this works for the cubic function $f(x) = x - x^3$ .

\begin{aligned} f'(x) &= \lim_{\Delta x \rightarrow 0} \frac{((x + \Delta x) - (x + \Delta x)^3) - (x - x^3)}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{((x + \Delta x) - (x^3 + 3x^2 \Delta x + 3x \Delta x^2 + \Delta x^3)) - (x - x^3)}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{((\Delta x) - (3x^2 \Delta x + 3x \Delta x^2 + \Delta x^3))}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} 1 - 3x^2 - 3x \Delta x - \Delta x^2 \\ &= 1 - 3x^2. \end{aligned}

In the first line, we just substituted $x + \Delta x$ for $x$ in the function, subtracted $f(x)$ and divided the whole thing by $\Delta x$ . The second line is the same, but with the cubic term expanded, and in the third line we subtract $f(x)$ from $f(x + \Delta x)$ which cancels out the term $x - x^3$ everywhere, leaving only terms that have $\Delta x$ in them.

In the fourth line, we divide by $\Delta x$ which leaves two terms without $\Delta x$ , and two with. Finally, taking the limit as $\Delta x$ gets close to zero, the last two terms become zero leaving only $f'(x) = 1 - 3x^2$ .

If you want Geogebra to do the expansion of $(x + \Delta x)^3$ , use Expand((x+d)^3) and remember that $d$ is being used in place of $\Delta x$ .

In Geogebra, define the function $f(x)$ which draws the green curve. Let the Geogebra CAS calculate the derivative, $f'(x)$ which it calls $g(x)$ and draws as the orange curve. At the origin, $f(0) = 0,$ $f'(0) = 1$ and the orange curve reaches a maximum of one at that point. This means that a line tangent to $f(x)$ at the origin has a slope of one, so for every unit change along the $x-$ axis there’s an equal unit rise along the $y-$ axis, which is shown in the light gray dotted line.

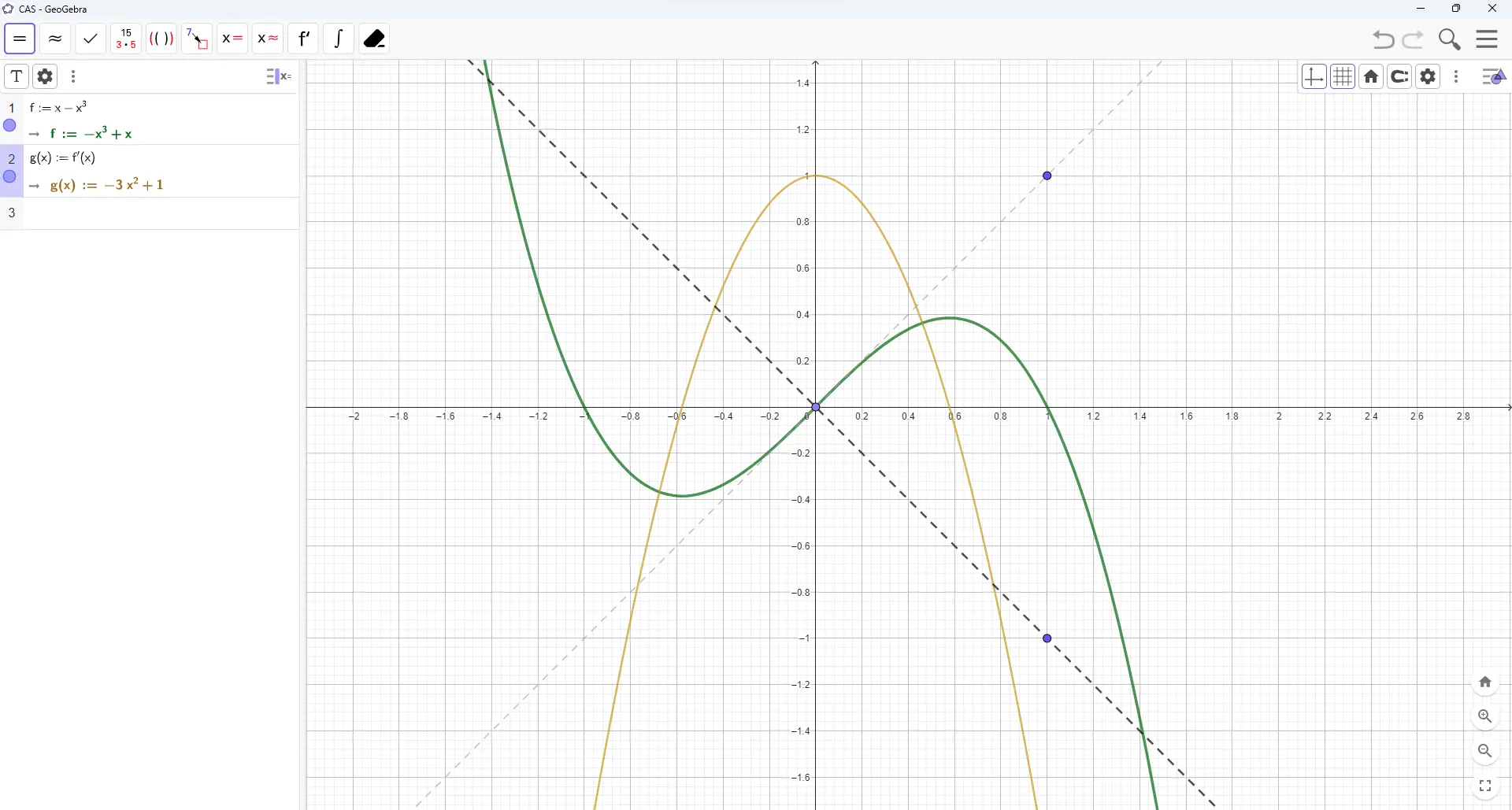
derivative-and-slope — Figure 3.
The function, derivative, tangent and perpendicular.

Two lines are perpendicular to each other if their slopes are negative inverses of each other. We often use the letter $m$ to denote the slope of a line, so the tangent at $f(0)$ has slope $m = 1$ , and a perpendicular will have slope $m = - \frac{1}{1} = -1$ . The perpendicular through the origin is shown in the darker dotted line.

Defining the problem

The center of the circle is somewhere on the line $y = -x$ and the distance from the center to the two points of contact with the function $f = x - x^3$ is the radius, $r$ . We need to find the point $G$ that represents the second point on the circle and the function.

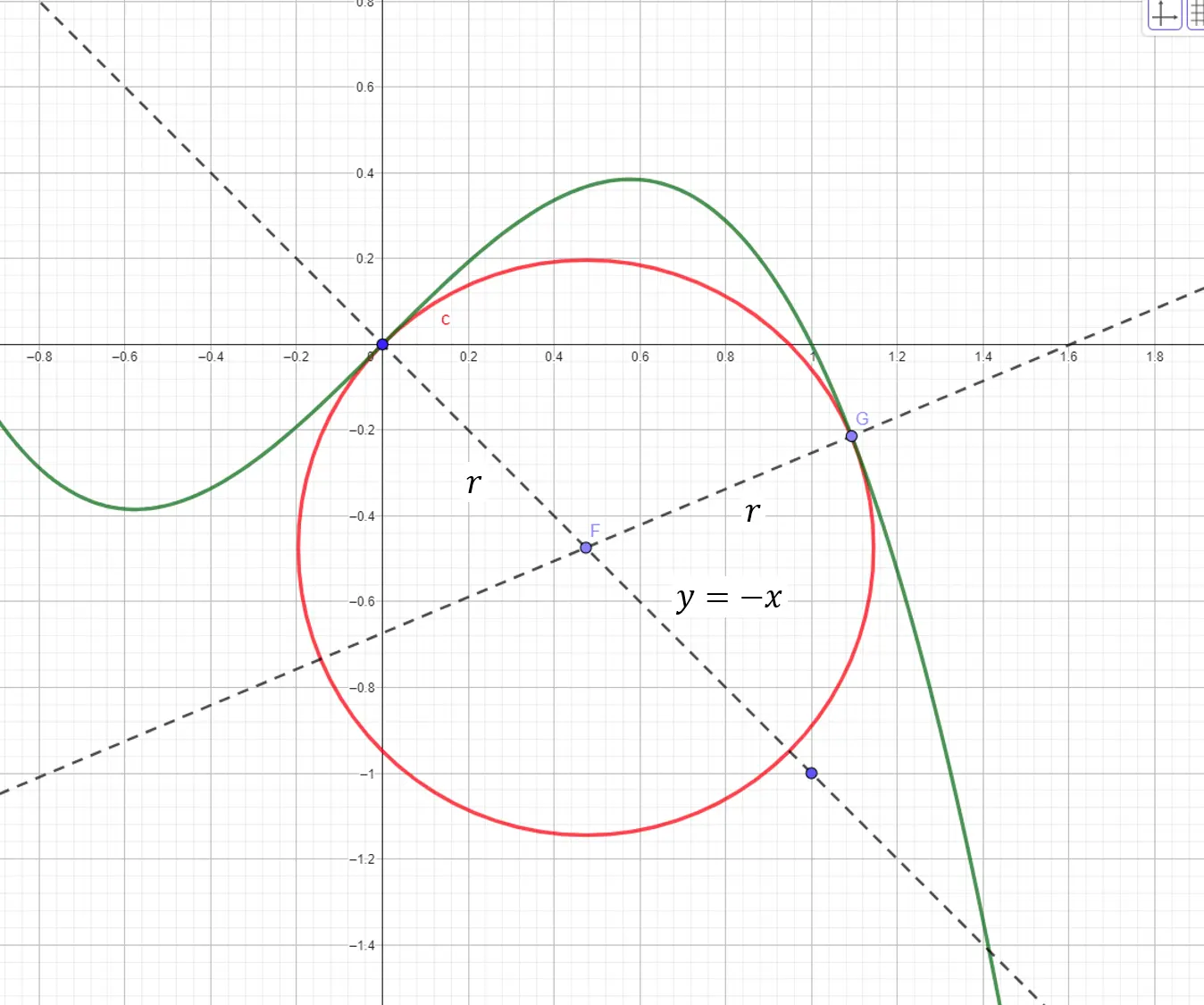
circle-center — Figure 4.
The center of the circle.

Since $F$ is on the line $y = -x$ , then the coordinates of $F$ are $(x_F,-x_F)$ and distance from $F$ to the origin is $r = \sqrt{x_F^2 + (-x_F)^2} = \sqrt{2}x_F$ . The point $G$ has coordinates $(x_G, x_G - x_G^3)$ and the slope of the perpendicular through $G$ is

m = -\frac{1}{1 - 3x_G^2}.

The equation of a line through $G$ with slope $m$ is

\begin{aligned} (y-y_G) &= m(x - x_G) \\ y &= m(x - x_G) + y_G. \\ \end{aligned}

Substituting for the slope $m$ ,

y = -\frac{1}{1 - 3x_G^2}(x - x_G) + y_G

and then for $y_G$ ,

y = -\frac{1}{1 - 3x_G^2}(x - x_G) + (x_G - 3x_G^2).

At the point of intersection $y$ equals $y_F$ which is $-x_F$ so the equation becomes

-x_F = -\frac{1}{1 - 3x_G^2}(x_F - x_G) + (x_G - 3x_G^2).

Since there are two unknowns, $x_F$ and $x_G$ we’ll need another equation, which is the equation for the radius. Using the Pythagorean theorem,

\begin{aligned} r &= \sqrt{2}x_F = \sqrt{(x_F - x_G)^2 + (y_F - y_G)^2} \\ &= \sqrt{(x_F - x_G)^2 + (-x_F - (x_G - 3x_G^2))^2}. \end{aligned}

Squaring both sides,

2x_F^2 = (x_F - x_G)^2 + (-x_F - (x_G - 3x_G^2))^2.

Now we have two equations and two unknowns, so we should be able to find a solution. Finding a closed form, or analytic solution is probably not possible, so we may have to settle for a numerical approximation.

The Geogebra solution

To solve the two equations simultaneously, enter the following in Geogebra:

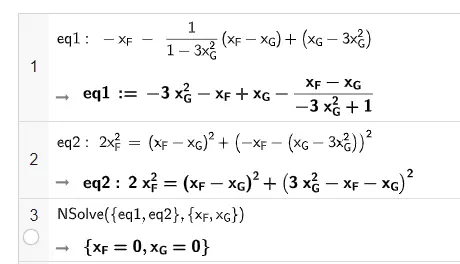
solution-at-origin — Figure 5.
The Geogebra solution.

and it gives a solution where both $x_F$ and $x_G$ are at the origin. In this case, the radius is zero, but obviously there’s another solution where $x_G > x_F$ .

The wxMaxima solution

The Geogebra CAS wasn’t able to provide a second solution for the point $G$ , but with a bit of rearrangement of the equations, wxMaxima found a solution for $x_F$ . Besides the cubic equation $f(x)$ and the derivative $f'(x) = df(x)$ , the equation for a line perpendicular to $f$ at any point $x_0$ can be defined as

L(x,x_0) = -\frac{1}{df(x_0)}(x-x_0) + f(x_0)

which is the $y = m(x-x_0) + y_0$ form for a line. With this, we can define the line through the origin as $L_1(x) = L(x,0)$ which intersects the line through the point $G$ at the point $F$ . The distances from $F$ to the origin and $F$ to $G$ are the radius $r$ of the circle which we can define as

\begin{aligned} d_1(x_0) &= x_0^2 + L_1(x_0)^2 \\ d_2(x_0,x_1) &= (x_0 - x_1)^2 + (L_1(x_0) - f(x_1))^2. \end{aligned}

In both, we didn’t take square roots but will require that they are equal (and equal to $r^2$ ). For $d_1$ , the distance is from the point $x_0$ to the origin, so we’re effectively subtracting $0$ from both the $x$ and $y$ terms. In the second equation, $d_2$ is the distance from $F$ to some point $G$ on the cubic function. The coordinates of $F$ are $(x_0,L_1(x_0))$ and the coordinates for $G$ are $(x_1, f(x_1))$ .

Entering these equations into wxMaxima and then asking for a solution gives this result:

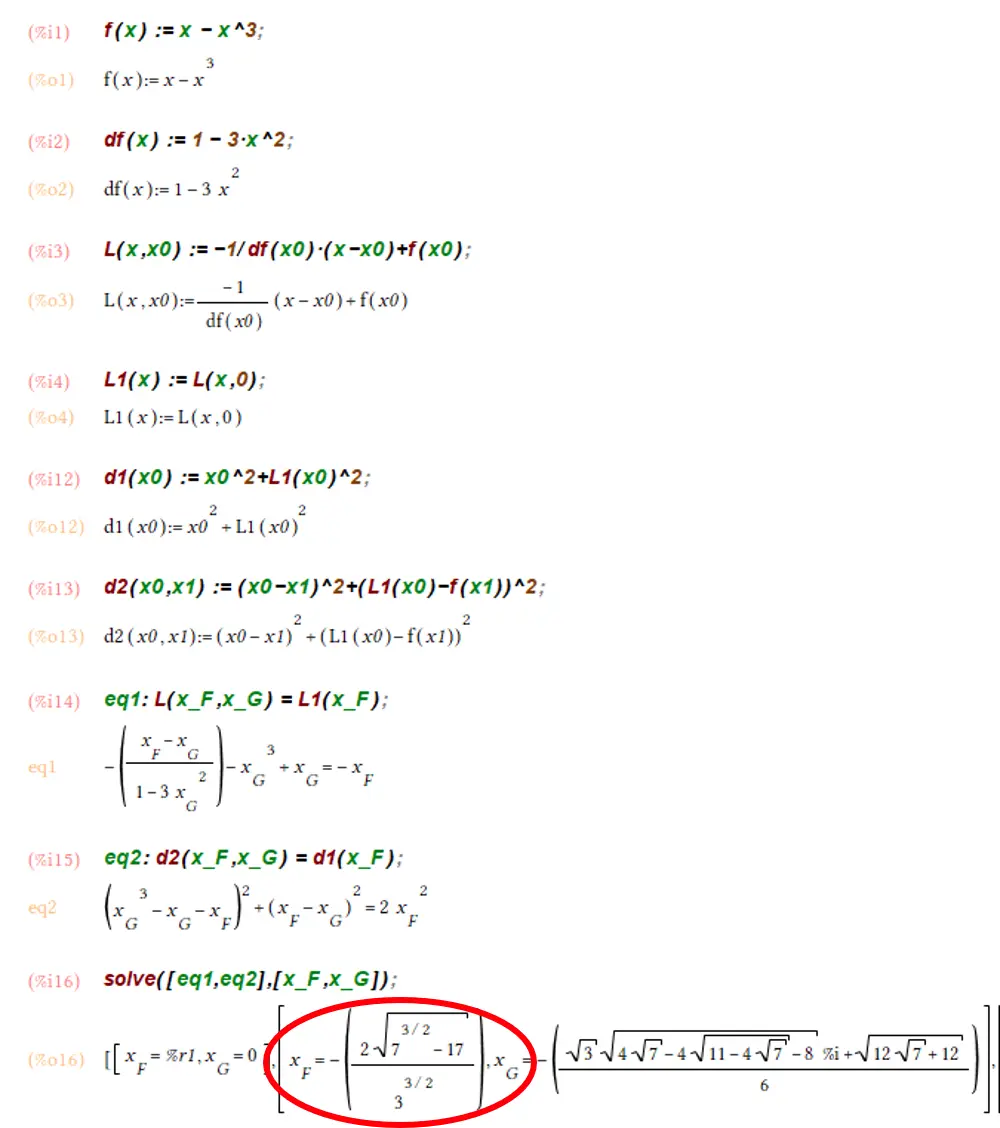
maxima-solution — Figure 6.
The wxMaxima solution.

There are two real roots to the problem from symmetry because the circle could have been flipped about the line $y=x$ , which is why $x_F$ is shown as a negative number here. Numerically, $x_F \approx 0.4745772664643349$ , and the radius of the circle is $r = \sqrt{2}x_F \approx 0.6711536066278128$ .

So, the Geogebra CAS wasn’t able to find two solutions, but the wxMaxima CAS found $x_F$ . Notice that the solution for $x_G$ contains $\%i$ , meaning that the point lies in the complex plane. Since the equation is a high order polynomial and there are only three real solutions, we should expect the remaining solutions to be complex. (In fact, there are four real solutions because the point at the origin is included in both the positive and negative solutions for $x_F$ .)

We’ll leave this problem here, but you could continue the exploration by finding the area of the circle, and the solution for $x_G$ .

Software

Geogebra - GeoGebra is dynamic mathematics software for all levels of education that brings together geometry, algebra, spreadsheets, graphing, statistics and calculus in one easy-to-use package.
Wolfram Language - Wolfram Language is a symbolic language, deliberately designed with the breadth and unity needed to develop powerful programs quickly.

Image credits

Hero: Spiral illusion is enough to give you a headache — here’s why, Natalie Wolchover, NBC News Sept. 11, 2012.
Curiosity Cats: Far Side, Gary Larson.