Lean into Math

A Concise Guide to Vibe Mathing

March 23, 2025 · John Peach

Andrej Karpathy who co-founded OpenAI coined the phrase vibe coding in February 2025 by which he meant that software engineers can use Large Language Models (LLMs) such as OpenAI’s ChatGPT to generate code from input prompts. “Vibe coding is claimed by its advocates to allow even amateur programmers to produce software without the extensive training and skills previously required for software engineering.” (Wikipedia - Vibe Coding)

The response from the community was not overwhelmingly positive. In the r/programming subreddit, Kush_238 asks, “Why ‘Vibe Coding’ Makes Me Want to Throw Up?” and some of the answers were:

Could this vibe idea be applied to mathematics? Can AI prove theorems? Yes, but even though these Large Language Models (LLMs) are constantly improving, they’re still prone to errors. After all, they were trained to understand and respond to language, not mathematics. What if we could improve the accuracy of LLMs by asking them to apply math tools rather than solving the problem directly? Why ask a language model to solve a math problem when you can use a calculator to provide the exact answer? Wolfram Alpha is available as an app for your phone and will accurately answer any questions you might ask.

Sometimes, to solve a problem you need to know the right substitution to make the solution possible, but even a good Computer Algebra System (CAS) like Mathematica (Wolfram Alpha is based on Mathematica) won’t be able to solve it. On the other hand, an LLM might provide an answer but you shouldn’t trust it without carefully checking the steps.

Let’s take a look at a tricky problem, and see if we can get an LLM to generate the steps needed to solve it with the help of a CAS or a theorem prover such as Lean. Combining actual thinking about the problem with an AI system and real math tools could be the path to vibe mathing.

A Tricky Problem

We want to solve for an integer n>0n > 0 such that

(n3)!−(n3−1)!=720(n3−1)2.(n^3)! - (n^3-1)! = 720(n^3-1)^2.

Wolfram Alpha couldn’t find a solution to this, but if you make a simple substitution the problem becomes much easier. Let p=n3−1p = n^3-1 so the equation simplifies to

(p+1)!−p!=720p2(p+1)! - p! = 720 p^2

and since (p+1)!=(p+1)p!(p+1)! = (p+1)p! the left side may be rewritten as

(p+1)p!−p!=720p2(p+1−1)p!=720p2pp!=720p2\begin{aligned} (p+1)p! - p! &= 720p^2 \\ (p+1-1)p! &= 720p^2 \\ pp! &= 720p^2 \end{aligned}

One solution is to let p=0p=0 so both sides become zero. If p≠0p \neq 0, then p!=720pp! = 720p, or (p−1)!=720(p-1)! = 720. The next step is to realize that 720=6!720 = 6! which means p−1=6p-1 = 6 or p=7.p = 7. So, now we have two solutions. Either p=0p=0 or p=7p=7 and solving for nn gives n=1n=1 or n=2.n=2.

Use your favorite CAS or other programming language (I used Pari/GP) to define two functions:

fL(n) = (n^3)! - (n^3-1)! 
fR(n) = 720(n^3-1)^2

For n=1n=1 both sides are zero since 1!=0!=11! = 0! = 1 and (13−1)=0(1^3 - 1) = 0. When n=2n=2 both sides equal 3528035280, so the solutions check.

Now let’s see if an LLM can solve the problem.

DeepSeek

DeepSeek is the latest LLM. It’s completely free to use and the code is fully open-source and is actively being blocked by governments around the world due to fears of excessive user data collection. Fine. I’ll bore them to tears with math problems. Here’s the prompt I used for the problem (Z+\Z^+ is shorthand for positive integers):

I want to use the Lean4 Theorem Prover to solve (n3)!−(n3−1)!=720(n3−1)2(n^3)! - (n^3-1)! = 720(n^3-1)^2 for n∈Z+n \in \Z^+. How should I set this up in Lean?

DeepSeek responded with a six-step outline that included required Lean libraries, but Deepseek thought the problem was to show that the equation holds for all nn. It tried n=1n=1 and showed it was a solution, and then it tried n=2n=2 and again found a solution. Step 5 was:

Step 5: General Proof (if possible)

If you want to prove the equation for all n∈Z+, you would need to find a general proof. However, this might not be straightforward, and you might need to use more advanced techniques or even prove that no other solutions exist beyond a certain point.

Finally, it wrote a Lean function to test other integers.

ChatGPT

ChatGPT by OpenAI has many specialized AI tools, one of them being Wolfram. The Wolfram GPT gave this solution:

We are given the equation:

(n3)!−(n3−1)!=720(n3−1)2(n^3)! - (n^3-1)! = 720(n^3-1)^2

Step 1: Factorial Factorization

Rewriting the factorial terms:

(n3)!=(n3)⋅(n3−1)!(n^3)! = (n^3) \cdot (n^3-1)!

Thus, substituting in the equation:

(n3)⋅(n3−1)!−(n3−1)!=720(n3−1)2(n^3) \cdot (n^3-1)! - (n^3-1)! = 720(n^3-1)^2

Factoring out (n3−1)!(n^3-1)!:

(n3−1)!⋅(n3−1)=720(n3−1)2(n^3-1)! \cdot (n^3 - 1) = 720(n^3-1)^2

Step 2: Canceling (n3−1)(n^3 - 1) When Possible

If n3−1≠0n^3 - 1 \neq 0, we divide by (n3−1)(n^3-1):

(n3−1)!=720(n3−1)(n^3-1)! = 720(n^3-1)

Step 3: Solving for nn

We now need to find integer values of nn such that:

(n3−1)!=720(n3−1)(n^3-1)! = 720(n^3-1)

Checking small values of nn:

  1. n=1n = 1: n3−1=0n^3 - 1 = 0, division is not possible.
  2. n=2n = 2: n3−1=7n^3 - 1 = 7 7!=5040,720×7=50407! = 5040, \quad 720 \times 7 = 5040 This is a valid solution.
  3. n=3n = 3: n3−1=26n^3 - 1 = 26 26!≠720×2626! \neq 720 \times 26 (26! is vastly larger than 1872018720, so this does not work.)

Since factorials grow extremely fast, checking larger values of nn will only increase the left-hand side much more than the right-hand side.

Conclusion

The only integer solution is:

n=2\boxed{n = 2}

This is almost correct, but it decided that n=1n=1 couldn’t be a solution because that might imply a division by zero. Let’s try a hybrid approach.

The Lean Theorem Prover

Lean is both a mathematical proof assistant and a computer language designed to help formalize mathematics. This means that every step of a proof can be checked rigorously. Mathematical concepts and proofs are translated into a language that a computer can understand and verify. Imagine writing a problem out on a whiteboard. Sooner or later, you’ll miss a minus sign, or make some other minor algebraic error and the proof will be incorrect. Lean takes the tedium out of the proof.

The advantage of both Lean and Mathematica is that they don’t hallucinate the way AI systems do, but a good AI can provide the syntax used in the mathematical software. For help setting up Lean and Mathematica, see our previous article, JupyterLab Desktop.

My initial prompt to ChatGPT was

How should the problem statement be entered into Lean4? Don’t try to solve the problem, just set it up.

It showed how to set the problem up, but it also asked if I wanted to restrict n∈Nn \in \N instead of all integers because the factorial function is not defined for negative numbers. In fact, Ashwani Thukral described a method for applying the factorial to both negative and imaginary numbers, but we’ll keep the original restriction of non-negative integers. ChatGPT also suggested that I set the problem up as a theorem to be proved, rather than a definition.

Here’s how you can write the problem as a theorem in Lean 4, phrased as the existence of a natural number nn satisfying the given equation:

import Mathlib.Data.Nat.Factorial.Basic
import Mathlib.Data.Nat.Basic

open Nat

theorem exists_solution_to_factorial_equation :
  ∃ n : ℕ, let k := n ^ 3
           k.factorial - (k - 1).factorial = 720 * (k - 1) ^ 2 :=
  sorry

Explanation:

You could also add an explicit condition like n ≥ 1 if you want to avoid dealing with edge cases like k−1=0k - 1 = 0.

Notice that ChatGPT made the substitution k=n3k = n^3, which is in the general direction of how I want to solve the problem, but I’d rather use the original substitution p+1=n3p+1 = n^3. Another prompt to ChatGPT gave this:

There are two adjustments needed for correctness in Lean 4 syntax:

  1. Lean does not allow arbitrary expressions like (n^3).factorial unless n^3 is explicitly defined as a natural number. So factorial must be applied to variables of type ℕ, and the whole expression must live in a Prop (like an equality or a ∃).
  2. You must quantify n : ℕ, since your theorem refers to an unspecified variable n.

Here is the corrected and idiomatic way to state it in Lean 4 without any substitutions:

import Mathlib.Data.Nat.Factorial.Basic
import Mathlib.Data.Nat.Basic

open Nat

theorem exists_solution_to_factorial_equation :
  ∃ n : ℕ, (n ^ 3) ! - (n ^ 3 - 1) ! = 720 * (n ^ 3 - 1) ^ 2 :=
  sorry

Notes:

Then, ChatGPT seemed to get stuck on the idea that all it needed to do was to show that n=1n=1 and n=2n=2 were solutions to the problem:

import Mathlib.Data.Nat.Factorial.Basic
import Mathlib.Data.Nat.Basic

open Nat

theorem all_solutions_to_factorial_equation :
  ∃ n : ℕ, (n ^ 3)! - (n ^ 3 - 1)! = 720 * (n ^ 3 - 1) ^ 2 :=
by
  -- Try n = 1
  use 1
  norm_num  -- (1^3)! - (0)! = 1 - 1 = 0, RHS = 720 * 0 = 0

  -- Try n = 2
  use 2
  norm_num  -- (8)! - (7)! = 40320 - 5040 = 35280, RHS = 720 * 49 = 35280

If I were more familiar with the syntax of Lean, I might be able to work around this. The Mechanics of Proof by Heather Macbeth and Mathematics in Lean by Jeremy Avigad and Patrick Massot are recommended on the Lean documentation site.

The Mathematica Solution

The syntax in Mathematica is a bit more similar to how you might write equations on a whiteboard. The first step is to define the equation,

eq = Factorial[n^3] - Factorial[n^3 - 1] == 720*(n^3 - 1)^2

which Mathematica rewrites as

n3!−(−1+n3)!==720(−1+n3)2.n^3! - (-1+n^3)! == 720(-1+n^3)^2.

Next, we substitute p=n3−1p = n^3 -1 with

eq1 = eq /. n^3 -> p + 1

Mathematica correctly generated −p!+(1−p)!==720p2-p! + (1-p)! == 720p^2. At this point, Mathematica began to break down. It couldn’t simplify this with the Reduce command, so I moved on to the last step, (p−1)!=720,(p-1)! = 720, and asked it to find the numerical answer,

NSolve[Factorial[p - 1] == 720, p]

which generated this result:

NSolve::ifun: Inverse functions are being used by NSolve, so some solutions may not be found; use Reduce for complete solution information.

p→7.37811+3.20076i.p \rightarrow 7.37811 + 3.20076 \mathcal{i}.

Curiously, WolframAlpha finds the correct solution, which we can use to solve for nn:

Solve[n^3 == 0 + 1 && n ∈ Integers && n ≥ 0, n]   
Solve[n^3 == 7 + 1 && n ∈ Integers && n ≥ 0, n]

returning n=1,2n = {1,2}. You can check that these answers are correct by substituting them into the original equation,

eq /. n -> 1
eq /. n -> 2

which will return True.

Prove-It

Several other theorem-proving systems have been developed, and one that might be worth a second look is Prove-It developed at Sandia National Laboratories. Prove-It is a Python-based interactive theorem-proving assistant designed to mirror informal mathematical reasoning in a JupyterLab Notebook. Prove-It focuses on human intuition in proof construction while supporting automation.

The system is organized into a hierarchical theory package system containing axioms, conjectures, and theorems with associated proofs, and it includes mechanisms to manage theorem dependencies and avoid logical paradoxes such as Russell’s or Curry’s. In their paper, the developers of Prove-It present a formalization of the classic proof that the square root of 2 is irrational and show its potential applications, including quantum computing verification.

The value of Prove-It may be that it generates output using LaTeX symbols bringing the system closer to a whiteboard experience.

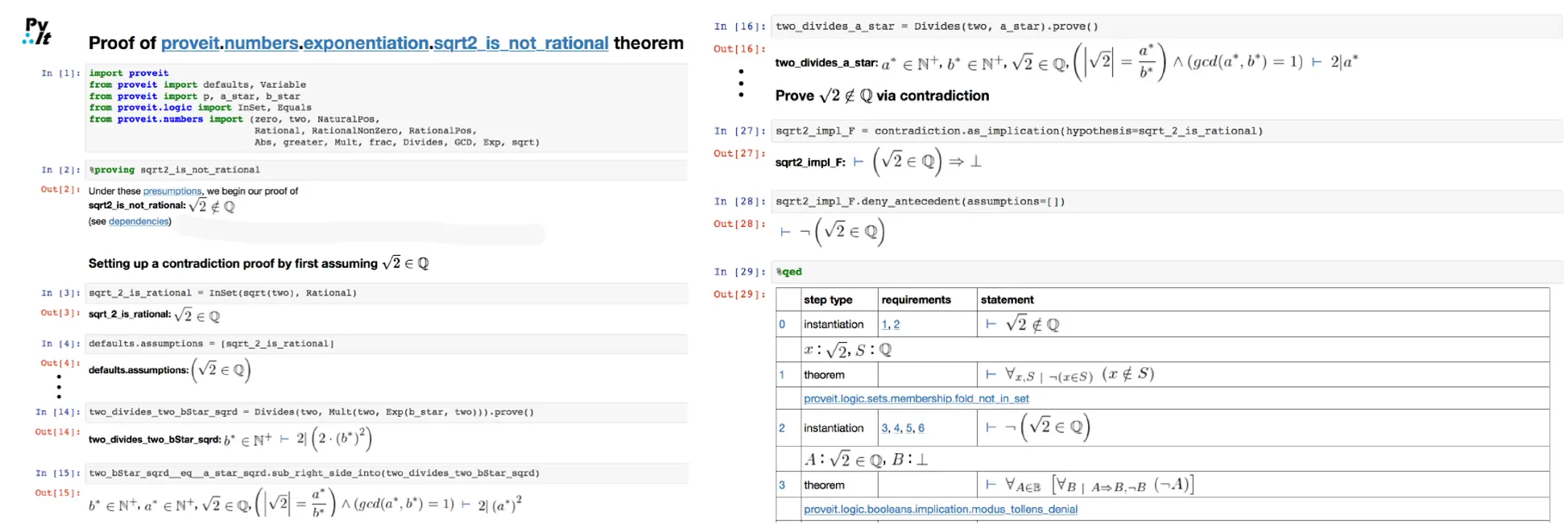
sqrt2-irrational
Figure 1.

The Prove-It interface.

Getting started with AI in mathematics

The value in vibe mathing is in checking your answers. Of course, most of the value comes from using a solid prover or Computer Algebra System (CAS), and not AI. A procedure for solving problems with these tools is:

You might try Andrej Karpathy’s method of asking AI to solve the problem and then iterating on the solution it provides. I asked Claude (Sonnet 3.5) on Poe and it somehow decided that the solution was n=73n = 7 \sqrt{3}. When I asked if n=1n=1 was a solution, it checked and found that it was, and then I repeated the question for n=2n=2. Again, it decided that this was a solution, but in the end, thought that all three answers: n={1,2,73}n = \{1,2, 7 \sqrt{3}\} satisfied the equality.

Wolfram Alpha wasn’t able to find any solution. Still, this may have been a tricky problem, and you may have more luck with another one. If you want to learn how to prove theorems, I recommend The Nuts and Bolts of Proofs by Antonella Cupillari (free online). You don’t need to write out theorems and their proofs formally the way mathematicians do, either. In fact, doing the algebra for a problem step-by-step is a form of proof.

With these thoughts in mind, happy vibe mathing!

Code for this article

The JupyterLab notebook for this article is on GitHub. This should give you a good starting point for any theorems you’d like to prove.

Software

References and further reading

Image credits